أمثلة على الأعداد الحقيقية والغير حقيقية
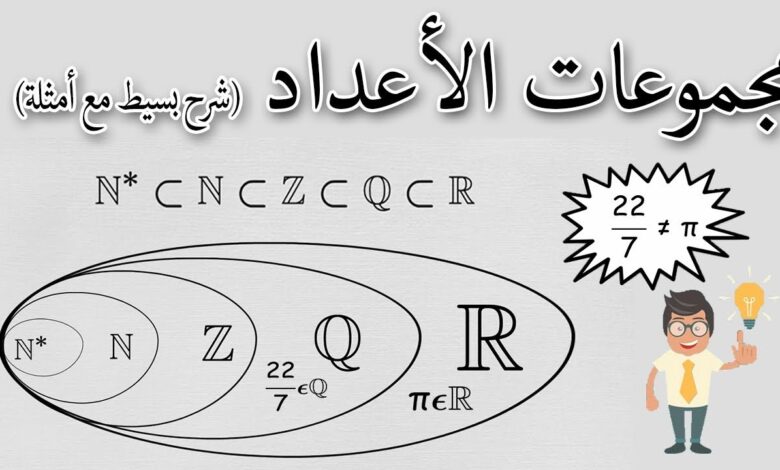
أمثلة على الأعداد الحقيقية والغير حقيقية في الرياضيات، العدد الحقيقي هو رقم يستخدم لقياس كميّة مستمرة أحادية البعد مثل المسافة أو المدة أو درجة الحرارة. يمكن تمثيل كل رقم حقيقي بشكل فريد تقريبًا من خلال توسيع عشري لانهائي. وفي السطور التالية نوضح كافة التفاصيل على موقع بسيط دوت كوم.
أمثلة على الأعداد الحقيقية
تعرف الأعداد الحقيقية بأنها الأعداد التي يمكن تمثيلها على خط الأعداد، وقد يكون العدد الحقيقي صحيح أو كسري، موجب أو سالب، فالمهم أن يكون مربّعه حقيقيًا موجبًا، ولا بدّ من الإشارة إلى أنّ حاصل عملية جمع أو ضرب عددين حقيقيين معًا هو عدد حقيقي بالضرورة. وتنقسم الأعداد الحقيقية إلى نوعين رئيسيين:
- الأعداد النسبية: وهي الأعداد التي يمكن تمثيلها ككسر، مثل 1/2 أو 3/4.
- الأعداد غير النسبية: وهي الأعداد التي لا يمكن تمثيلها ككسر، مثل جذر 2 أو جذر 3.
خصائص الأعداد الحقيقية
تتمتع الأعداد الحقيقية بالعديد من الخصائص، من أهمها:
- الاستمرارية: يمكن العثور على أي عدد حقيقي بين أي عددين حقيقيين.
- الجمع: جمع أي عددين حقيقيين هو عدد حقيقي.
- الضرب: ضرب أي عددين حقيقيين هو عدد حقيقي.
- القسمة: يمكن قسمة أي عدد حقيقي على أي عدد حقيقي غير صفري.
- المقارنة: يمكن مقارنة أي عددين حقيقيين.
تطبيقات الأعداد الحقيقية
تستخدم الأعداد الحقيقية في العديد من التطبيقات في الرياضيات والعلوم والهندسة، من أهمها:
- حساب المسافات والزوايا والكميات الأخرى في الهندسة.
- حل المعادلات والأنظمة الخطية وغير الخطية.
- دراسة الدوال والعلاقات الرياضية.
- تمثيل البيانات والقياسات.
أمثلة على الأعداد الحقيقية والغير حقيقية
فيما يلي بعض أمثلة على الأعداد الحقيقية والغير حقيقية:
- العدد 0
- ثم الأعداد الطبيعية
- ثم الأعداد الصحيحة
- الأعداد الكسرية
- الأعداد غير النسبية.
جدير بالذكر الأعداد الحقيقية هي مجموعة لا نهائية من الأرقام التي يمكن استخدامها لتمثيل أي كميّة مستمرة في العالم الحقيقي. تتمتع الأعداد الحقيقية بالعديد من الخصائص التي تجعلها أداة قوية للرياضيات والعلوم والهندسة.
كيف اعرف الاعداد الحقيقية؟
يمكن معرفة الأعداد الحقيقية من خلال تعريفها، حيث تُعرَّف الأعداد الحقيقية بأنها جميع الأعداد التي يمكن العثور عليها على خط الأعداد، وهي تشمل الأعداد النسبية وغير النسبية، والموجبة والسالبة، وحتى الصفر. فيما يلي بعض الخصائص التي تحدد الأعداد الحقيقية:
- يمكن تمثيل الأعداد الحقيقية على خط الأعداد.
- ثم يمكن إجراء العمليات الحسابية الأساسية على الأعداد الحقيقية، مثل الجمع والطرح والضرب والقسمة.
- يمكن ترتيب الأعداد الحقيقية بشكل تصاعدي أو تنازلي.
أمثلة على الأعداد الحقيقية الصف الرابع
يمكن أيضًا معرفة الأعداد الحقيقية من خلال أمثلة منها، حيث تشمل الأعداد الحقيقية:
- الأعداد الطبيعية: 1، 2، 3، 4، …
- الأعداد الصحيحة: …، -3، -2، -1، 0، 1، 2، 3، …
- ثم الأعداد الكسرية: 1/2، 3/4، 5/6، …
- ثم الأعداد غير النسبية: √2، √3، √5، …
أمثلة على الأعداد الحقيقية الصف الخامس
فيما يلي بعض الأمثلة على الأعداد الحقيقية للصف الرابع والخامس:
- الارتفاع فوق مستوى سطح البحر: 100 متر، -100 متر، 0 متر.
- درجة الحرارة: 20 درجة مئوية، -20 درجة مئوية، 0 درجة مئوية.
- الوزن: 50 كيلوجرام، -50 كيلوجرام، 0 كيلوجرام.
- الوقت: 10:00 صباحًا، -10:00 صباحًا، 0:00 صباحًا. وبشكل عام، يمكن القول أن أي رقم يمكن تمثيله على خط الأعداد هو رقم حقيقي.
ما هي الاعداد الحقيقيه والغير حقيقيه؟
الأعداد الحقيقية هي مجموعة من الأرقام التي يمكن تمثيلها على خط الأعداد، وهي تشمل الأعداد النسبية والغير النسبية، والموجبة والسالبة، وحتى الصفر.
الأعداد غير الحقيقية هي مجموعة من الأرقام التي لا يمكن تمثيلها على خط الأعداد، وهي تشمل الأعداد التخيلية، مثل √-1 و 2 + 3i و -i.
تعريف الأعداد الحقيقية
الأعداد الحقيقية هي مجموعة من الأرقام التي تلبي الخصائص التالية:
- يمكن تمثيلها على خط الأعداد.
- ثم يمكن استخدامها في جميع العمليات الحسابية الأساسية، مثل الجمع والطرح والضرب والقسمة.
- ثم لها خصائص معينة، مثل خصائص التبديلية والجمع والتوزيعية.
أنواع الأعداد الحقيقية
الأعداد الحقيقية تنقسم إلى نوعين رئيسيين:
- الأعداد النسبية: هي الأعداد التي يمكن التعبير عنها ككسر، مثل 1/2 و 3/4 و 5/6.
- ثم الأعداد غير النسبية: هي الأعداد التي لا يمكن التعبير عنها ككسر، مثل √2 و √3 و √5.
تعريف الأعداد غير الحقيقية
الأعداد غير الحقيقية هي مجموعة من الأرقام التي لا يمكن تمثيلها على خط الأعداد، وهي تشمل الأعداد التخيلية.
الأعداد التخيلية
إن الأعداد التخيلية هي الأعداد التي تحتوي على وحدة تخيلية، وهي الحرف “i”. وتُعرف الأعداد التخيلية أيضًا بالأعداد العقدية.
خصائص الأعداد التخيلية
الأعداد التخيلية لها خصائص معينة نوضحها في صورة أمثلة على الأعداد الحقيقية، مثل:
- يمكن تمثيلها على خط الأعداد المركبة.
- ثم يمكن استخدامها في جميع العمليات الحسابية الأساسية، مثل الجمع والطرح والضرب والقسمة.
- ثم لها خصائص معينة، مثل خصائص التبديلية والجمع والتوزيعية.
استخدامات الأعداد الحقيقية والأعداد غير الحقيقية
تستخدم الأعداد الحقيقية في العديد من المجالات، مثل الرياضيات والفيزياء والهندسة. وتستخدم الأعداد التخيلية في مجال الهندسة الكهربائية والمعادلات التربيعية.
هل كل الاعداد اعداد حقيقية؟
لا، ليست كل الأعداد أعداد حقيقية. مجموعة الأعداد الحقيقية هي مجموعة ضخمة تحتوي على جميع الأعداد التي يمكن تصورها، بما في ذلك الأعداد الكسرية والغير كسرية، والأعداد الموجبة والسالبة، والصفر. هناك بعض الأعداد التي لا تنتمي إلى مجموعة الأعداد الحقيقية، مثل:
- الأعداد غير المحددة، مثل √-1.
- ثم الأعداد اللانهائية، مثل ∞.
- ثم الأعداد غير المنطقية، مثل π.
لذلك، يمكن القول أن الإجابة على سؤالك هي “لا، ليست كل الأعداد أعداد حقيقية”.
أمثلة على الأعداد الحقيقية الصف الخامس
فيما يلي بعض الأمثلة على الأعداد التي لا تنتمي إلى مجموعة الأعداد الحقيقية:
- √-1: هو عدد غير حقيقي لأنه لا يمكن كتابته بصيغة كسر عادي أو كعدد عشري.
- ∞: هو عدد غير حقيقي لأنه لا يمكن تمثيله على خط الأعداد.
- π: هو عدد غير حقيقي لأنه غير منطقي، أي أنه لا يمكن التعبير عنه بصيغة كسر عادي.
من الجدير بالذكر أن بعض علماء الرياضيات يعتبرون أن الأعداد غير المحددة واللانهائية هي أعداد حقيقية، ولكن هذا لا يزال موضع نقاش.
الفرق بين الكسر و العدد الكسري
الكسر هو مفهوم مجرد، بينما العدد الكسري هو طريقة لتمثيل الكسر. على سبيل المثال، العدد الكسري 2/3 هو طريقة لتمثيل الكسر الذي يمثل 2 جزء من أصل 3 أجزاء.
كيف تقسم الاعداد الكسرية؟
القسمة على عدد كسري تعادل الضرب في مقلوبه. للحصول على مقلوب عدد كسري، يجب عكس البسط والمقام. على سبيل المثال، مقلوب العدد الكسري 5/7 هو 7/5. على سبيل المثال، لقسمة 3/4 على 2/3، نقوم بالخطوات التالية:
- نقوم بعكس البسط والمقام للكسر الثاني: 2/3 يصبح 3/2.
- نقوم بالضرب في الكسور: 3/4 * 3/2 = 9/8.
أي الاعداد الكسرية التالية يمثل الكسر 11 4؟
الكسر 11 4 هو كسر عادي، أي أنه يمثل قسمة عددين صحيحين. في هذه الحالة، يكون العدد الصحيح في البسط هو 11، والعدد الصحيح في المقام هو 4.
أي عدد كسري يكون له نفس البسط والمقام مع الكسر 11 4 سيمثل نفس الكسر. لذلك، فإن الاعداد الكسرية التالية تمثل جميعها الكسر 11 4:
- 11/4 هو التعبير الأصلي للكسر.
- 75 هو التعبير العشري للكسر.
- 55/20 هو تعبير آخر للكسر ببساطة عن طريق إعادة ترتيب البسط والمقام.
- 22/8 هو تعبير آخر للكسر ببساطة عن طريق قسمة البسط والمقام على 2.
- 110/40 هو تعبير آخر للكسر ببساطة عن طريق قسمة البسط والمقام على 4.
كيف يتم ضرب الاعداد الكسرية؟
يتم ضرب الأعداد الكسرية عن طريق ضرب البسط والمقام لكل كسر على حدة، ثم وضع البسط الناتج في كسر جديد يكون مقامه حاصل ضرب المقامين الأصليين. على سبيل المثال، لضرب كسرين هما 2/3 و 4/5، نقوم بما يلي:
- ضرب البسط الأول بالمقام الثاني: 2 * 5 = 10
- ضرب البسط الثاني بالمقام الأول: 4 * 3 = 12
- ثم وضع البسط الناتج في كسر جديد يكون مقامه حاصل ضرب المقامين الأصليين: 10/12 وبالتالي، فإن ناتج ضرب 2/3 و 4/5 هو 10/12، أو 5/6.
ضرب الأعداد الكسرية
ضمن الحديث عن أمثلة على الأعداد الحقيقية يمكن أيضًا ضرب الأعداد الكسرية باستخدام الاختصار التالي:
- ضع البسط الأول فوق البسط الثاني: 2/3
- ضع المقام الأول تحت المقام الثاني: 3/5
- ثم اضرب الأرقام في كل عمود: 2 * 4 = 8
- ثم اضرب المقامات: 3 * 5 = 15
- ضع الناتج في كسر جديد يكون مقامه 15: 8/15
- وبالتالي، فإن ناتج ضرب 2/3 و 4/5 هو أيضًا 8/15.
أمثلة على ضرب الكسور
فيما يلي بعض الأمثلة على ضرب الأعداد الكسرية:
- 2/3 * 4/5 = 8/15
- 3/4 * 5/6 = 15/24
- 1/2 * 1/3 = 1/6
- 1/5 * 1/6 = 1/30
- 1/10 * 1/11 = 1/110
هل كل عدد صحيح هو عدد كسري؟
نعم، كل عدد صحيح هو عدد كسري. الكسر هو عدد يمكن التعبير عنه في صورة النسبة بين عددين صحيحين، بحيث لا يكون المقام مساوياً للصفر. على سبيل المثال، العدد الصحيح 5 يمكن التعبير عنه في صورة الكسر 5/1، والعدد الصحيح -3 يمكن التعبير عنه في صورة الكسر -3/1.
ومع ذلك، فإن العكس ليس صحيحًا، أي أن ليس كل كسر هو عدد صحيح. على سبيل المثال، الكسر 1/2 ليس عددًا صحيحًا، لأنه لا يمكن التعبير عنه في صورة عدد صحيح من الوحدات. باختصار، فإن مجموعة الأعداد الصحيحة هي مجموعة فرعية من مجموعة الأعداد الكسرية.
الاعداد الكسرية للصف الرابع
الاعداد الكسرية هي اعداد يتم التعبير عنها على شكل كسر، ويتكون الكسر من جزأين:
- البسط: وهو الجزء العلوي من الكسر ويمثل عدد الأجزاء التي تم أخذها من الكل.
- المقام: وهو الجزء السفلي من الكسر ويمثل عدد الأجزاء التي تم تقسيم الكل عليها.
على سبيل المثال، الكسر 1/2 يمثل جزءًا واحدًا من قسمين. في الصف الرابع، يتعلم الطلاب التعرف على الاعداد الكسرية وكيفية تمثيلها، بالإضافة إلى كيفية إجراء العمليات الحسابية على الكسور.
أمثلة على الاعداد العشرية في الحياة اليومية
ضمن الحديث عن أمثلة على الأعداد الحقيقية فيما يلي بعض الأمثلة على استخدام الأعداد العشرية في الحياة اليومية:
- عند شراء سلعة من المتجر، نقوم بدفع مبلغ معين من المال. هذا المبلغ يتكون من عدد صحيح من الوحدات النقدية وعدد عشري من السنتات.
- عند قياس درجة الحرارة، نستخدم مقياس الحرارة الذي يعرض درجة الحرارة على شكل رقم عشري.
- ثم عند قياس المسافة، نستخدم المسطرة أو الميزان الذي يعرض المسافة على شكل رقم عشري.
- الأعداد العشرية هي جزء أساسي من الرياضيات، وتستخدم في العديد من المجالات في الحياة اليومية.
كم يساوي العشر بالارقام؟
العشر يساوي 10 بالأرقام. ويكتب العشر في اللغة العربية بحرف ع (عشرة) أو عَشْر (عشر). ثم أما في اللغة الإنجليزية، فيُكتب العشر بحرف 10 (ten). وبالتالي، فإن العشر يساوي 10 بالأرقام في كل من اللغتين العربية والإنجليزية.
ما هو جدول العد العشري؟
جدول العد العشري هو جدول يوضح ترتيب الأعداد العشرية من 0 إلى 9، ويستخدم لكتابة الأعداد العشرية. يتكون الجدول من 10 أعمدة، كل عمود يمثل منزلة معينة في العدد العشري. الأعمدة من اليسار إلى اليمين هي:
- منزلة الواحدات
- منزلة العشرات
- ثم منزلة المئات
- ثم منزلة الآلاف
- منزلة عشرات الآلاف
- منزلة مئات الآلاف
- ثم منزلة ملايين
- ثم منزلة عشرات الملايين
- منزلة مئات الملايين.
يمثل الرقم الموجود في كل عمود قيمة محددة، حيث أن الرقم 0 يمثل صفر، والرقم 1 يمثل واحد، والرقم 2 يمثل اثنين، وهكذا.
يستخدم جدول العد العشري لكتابة الأعداد العشرية، حيث يتم وضع الرقم المناسب في كل منزلة. على سبيل المثال، العدد 12.345 يكتب على النحو التالي:
1 | 2 | . | 3 | 4 | 5
أمثلة على الاعداد العشرية
- الرقم 1 يمثل منزلة الواحدات
- الرقم 2 يمثل منزلة العشرات
- النقطة العشرية تفصل بين الجزء الصحيح والجزء العشري
- ثم الرقم 3 يمثل منزلة العشرات العشرية
- ثم الرقم 4 يمثل منزلة المئات العشرية
- الرقم 5 يمثل منزلة الآلاف العشرية.
يمكن استخدام جدول العد العشري أيضًا لقراءة الأعداد العشرية، حيث يتم قراءة الرقم الموجود في كل منزلة من اليسار إلى اليمين. على سبيل المثال، العدد 12.345 يقرأ على النحو التالي:
اثنا عشر وثلاثة وعشرون جزءًا من مائة وثلاثة وعشرون جزءًا من ألف وخمسة وعشرون جزءًا من عشرة آلاف. ثم جدول العد العشري هو أداة مفيدة لكتابة وقراءة الأعداد العشرية.
ما معنى كلمة عدد عشري؟
كلمة “عدد عشري” تعني عددًا يمكن كتابته بالضبط بعدد منتهي الأرقام بعد الفاصلة، بواسطة نظام العد الهندي العربي. الأعداد العشرية عبارة عن قسمة عدد صحيح بواسطة رفع 10 وتمثل على شكل عدد كسري. يمكن كتابة الأعداد العشرية بعدة طرق، منها:
- الطريقة التقليدية: وهي كتابة العدد بالأرقام العربية، مع وضع الفاصلة العشرية بين الجزء الصحيح والجزء العشري.
- الطريقة الكسورية: وهي كتابة العدد على شكل عدد صحيح مقسوم على 10 مرفوع إلى قوة معينة، بحيث تكون هذه القوة مساوية لعدد الأرقام الموجودة بعد الفاصلة العشرية.
- ثم الطريقة العلمية: وهي كتابة العدد على شكل عدد صحيح مضروب في 10 مرفوع إلى قوة معينة، بحيث تكون هذه القوة موجبة إذا كان الجزء العشري موجبًا، وسلبية إذا كان الجزء العشري سالبًا.
ما هي الأعداد الطبيعية والصحيحة والنسبية؟
الأعداد الطبيعية هي الأعداد التي تبدأ من 1 وتستمر إلى ما لا نهاية، وهي لا تشمل الأعداد السالبة أو الصفر. ويرمز لمجموعة الأعداد الطبيعية بالحرف اللاتيني N. والأعداد الصحيحة هي الأعداد التي تشمل الأعداد الطبيعية والسالبة والصفر. ويرمز لمجموعة الأعداد الصحيحة بالرمز Z.
الأعداد النسبية هي الأعداد التي يمكن كتابتها على شكل كسر، حيث يكون بسط الكسر عددًا صحيحًا، ومقامه عددًا صحيحًا غير صفري. ويرمز لمجموعة الأعداد النسبية بالرمز Q. العلاقات بين الأعداد الطبيعية والصحيحة والنسبية:
- جميع الأعداد الطبيعية هي أعداد صحيحة.
- ثم جميع الأعداد الصحيحة غير السالبة هي أعداد طبيعية.
- ثم جميع الأعداد النسبية هي أعداد صحيحة أو أعداد طبيعية.
أمثلة على الأعداد الطبيعية والصحيحة والنسبية
- الأعداد الطبيعية: 1، 2، 3، 4، 5، …
- ثم الأعداد الصحيحة: -5، -4، -3، -2، -1، 0، 1، 2، 3، 4، 5، …
- ثم الأعداد النسبية: 1/2، 1/3، 2/3، -1/2، -1/3، -2/3، 0.5، 0.3333…، -0.5، -0.3333…
استخدامات الاعداد الصحيحة الطبيعية
- تستخدم الأعداد الطبيعية في العد والقياس.
- ثم تستخدم الأعداد الصحيحة في العمليات الحسابية.
- ثم تستخدم الأعداد النسبية في التعبير عن الأجزاء من الكل.
- الأعداد الطبيعية هي الأعداد التي تبدأ من 1 وتستمر إلى ما لا نهاية.
- ثم الأعداد الصحيحة هي الأعداد التي تشمل الأعداد الطبيعية والسالبة والصفر.
- ثم الأعداد النسبية هي الأعداد التي يمكن كتابتها على شكل كسر.
ما هي الأعداد الصحيحة والحقيقية والطبيعية؟
الأعداد الصحيحة هي مجموعة من الأعداد التي يمكن كتابتها بدون استخدام الكسور أو الفواصل العشرية. وتتكون مجموعة الأعداد الصحيحة من الأعداد الطبيعية (1، 2، 3.) والصفر والأعداد السالبة المقابلة للأعداد الطبيعية (-1، -2، -3..)
جدير بالذكر الأعداد الطبيعية هي مجموعة من الأعداد التي تبدأ بالرقم 1 وتستمر إلى ما لا نهاية. وتستخدم الأعداد الطبيعية لوصف الكميات المتناهية، مثل عدد الأشياء أو عدد المرات.
الأعداد الحقيقية هي مجموعة من الأعداد التي يمكن كتابتها باستخدام الكسور أو الفواصل العشرية. وتتكون مجموعة الأعداد الحقيقية من الأعداد الصحيحة والكسرية.
أنواع الاعداد الصحيحة الطبيعية
ضمن الحديث عن أمثلة على الأعداد الحقيقية فيما يلي شرح أكثر تفصيلاً لكل نوع من أنواع الأعداد:
الأعداد الصحيحة
- يمكن كتابتها بدون استخدام الكسور أو الفواصل العشرية.
- تتكون من الأعداد الطبيعية والصفر والأعداد السالبة.
- ثم الأعداد الطبيعية هي مجموعة فرعية من الأعداد الصحيحة.
- ثم الأعداد السالبة هي الأعداد الصحيحة التي تقل عن الصفر.
الأعداد الطبيعية
- تبدأ بالرقم 1 وتستمر إلى ما لا نهاية.
- ثم تستخدم لوصف الكميات المتناهية، مثل عدد الأشياء أو عدد المرات.
- ثم الأعداد الطبيعية هي مجموعة فرعية من الأعداد الصحيحة.
ما هي الأعداد الحقيقية؟
- يمكن كتابتها باستخدام الكسور أو الفواصل العشرية.
- تتكون من الأعداد الصحيحة والكسرية.
- ثم الأعداد الصحيحة هي مجموعة فرعية من الأعداد الحقيقية.
- ثم الأعداد الكسرية هي الأعداد التي يمكن كتابتها ككسر، مثل 1/2 أو 3/4.
من أمثلة الأعداد النسبية؟
من الأمثلة على الأعداد النسبية:
- الأعداد الطبيعية مثل 1، 2، 3، …
- ثم الأعداد الصحيحة مثل 0، -1، -2، …
- ثم الكسور مثل 1/2، 3/4، -5/6، …
- الأعداد العشرية المنتهية مثل 0.5، 2.345، -1.234، …
- ثم الأعداد العشرية الدورية مثل 0.33333…، 1/3، -1/9، …
بشكل عام، أي عدد يمكن كتابته على صورة كسر ﺃ/ﺏ، حيث ﺃ وﺏ عددان صحيحان وﺏ لا يساوي صفرًا، فهو عدد نسبي.
أمثلة على الأعداد الحقيقية والنسبية
فيما يلي بعض الأمثلة على الأعداد النسبية والحقيقية:
- العدد 3 هو عدد طبيعي، وهو أيضًا عدد صحيح، وبالتالي فهو عدد نسبي.
- ثم العدد -2 هو عدد صحيح، وبالتالي فهو عدد نسبي.
- ثم العدد 1/2 هو كسر، وبالتالي فهو عدد نسبي.
- العدد 0.5 هو عدد عشري منتهٍ، وبالتالي فهو عدد نسبي.
- ثم العدد 0.33333… هو عدد عشري دوري، وبالتالي فهو عدد نسبي.
يمكننا أيضًا أن نقول أن أي عدد يمكن التعبير عنه على شكل كسر ﺃ/ﺏ، حيث ﺃ وﺏ عددان صحيحان وﺏ لا يساوي صفرًا، فهو عدد نسبي. على سبيل المثال، يمكننا كتابة العدد 3 على شكل كسر 3/1، ويمكننا كتابة العدد -2 على شكل كسر -2/1، ويمكننا كتابة العدد 1/2 على شكل كسر 1/2، ويمكننا كتابة العدد 0.5 على شكل كسر 5/10، ويمكننا كتابة العدد 0.33333… على شكل كسر 1/3. وبالتالي، فإن جميع الأعداد المذكورة أعلاه هي أعداد نسبية.
قد يهمك





