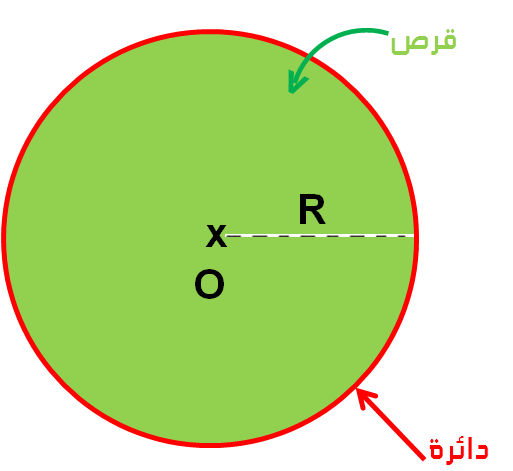
ما هو شعاع الدائرة
مقدمة
كمهندس مبتدئ أو طالب في مجال الهندسة، قد يثير طلب الدائرة تساؤلات عديدة في ذهنك. فما هو بالضبط شعاع الدائرة وكيف يؤثر في الهندسة؟
مفهوم الدائرة وأهميتها في الهندسة
الدائرة هي أحد أشكال الهندسة الأساسية وهي مجموعة من النقاط في المستوى تبعد جميعها بنفس المسافة عن نقطة مركزية. يتم تحديد شعاع الدائرة بواسطة خط يربط النقطة المركزية بأي نقطة على حافة الدائرة. يعد الشعاع مسافة الخط من المركز إلى الحافة ويمثل نصف قطر الدائرة.
يحمل الشعاع أهمية كبيرة في الهندسة. فهو يستخدم في حسابات الأبعاد والمسافات في العديد من التطبيقات الهندسية مثل تصميم الهياكل، والهندسة المعمارية، والرسوم الفنية، وحسابات الدقة. يساعد مفهوم الشعاع أيضًا على فهم خصائص الدوائر والمساحات المحيطة وحجم المجسمات الدائرية.
لذا، فإن فهم مفهوم الدائرة وشعاعها سيساعدك على التعامل بكفاءة مع المسائل الهندسية المتعلقة بها وتطبيقها في تصاميمك وحساباتك المستقبلية.
تعريف شعاع الدائرة
يعد شعاع الدائرة من المصطلحات الأساسية في الهندسة الهندسة المشهورة. في الأساس ، يمثل الشعاع جزءًا من الدائرة يبدأ من مركز الدائرة ويمتد إلى أي نقطة على حافتها، وهو جزء من المستقيم الذي يربط المركز بالنقطة المحددة. عبارة عن خط مستقيم يحدد أحد حواف الدائرة ويتم تسميته عادةً بالحرف “ر” كرمز لكلمة “راي”. يعتبر الشعاع من العناصر الأساسية في تحديد خصائص الدائرة.
تعريف شعاع الدائرة ودوره في تمييز الدائرة
يمتلك الشعاع دورًا هامًا في تمييز الدائرة وتحديد خصائصها. عند تحديد الدائرة ، يكون لكل شعاع خصائص فريدة تميزه عن غيره. يتم استخدام الشعاع في قياسات الدائرة ، حيث يوفر معلومات حول نصف قطر الدائرة وقطرها ومحيطها ومساحتها. بفضل الشعاع ، يمكن للمهندسين والعلماء فهم ودراسة الدوائر وتحليل خصائصها.
في الختام ، فإن الشعاع هو جزء ضروري من الدائرة ويساهم في تعريفها وتمييزها. يلعب الشعاع دورًا حاسمًا في إظهار الخصائص الفريدة للدائرة واستخدامها في القياسات والتحليل
استخدامات شعاع الدائرة
شعاع الدائرة هو مصطلح يستخدم في الرياضيات لوصف مستقيم يبدأ من مركز الدائرة ويصل إلى طرفها. يعد شعاع الدائرة أحد العناصر الهامة في دراسة الدوائر والمسائل المتعلقة بها. فيما يلي بعض الاستخدامات الشائعة لشعاع الدائرة:
استخدام شعاع الدائرة في حسابات الدوائر ومعادلاتها
تستخدم شعاع الدائرة في العديد من الحسابات والمعادلات المتعلقة بالدوائر. على سبيل المثال، يمكن استخدام شعاع الدائرة لحساب طول القوس في دائرة ما، وذلك باستخدام الزاوية المركزية ونصف قطر الدائرة. كما يمكن استخدامه لحساب مساحة القطاع في دائرة ما، وذلك باستخدام الزاوية المركزية ونصف قطر الدائرة.
بالإضافة إلى ذلك، يمكن استخدام شعاع الدائرة في حل المعادلات المتعلقة بالدوائر. على سبيل المثال، إذا كان لديك معادلة تمثل مساحة دائرة، يمكن استخدام شعاع الدائرة لحل المعادلة وتحديد قيمة نصف قطر الدائرة.
باختصار، يعد شعاع الدائرة أداة مفيدة في حسابات الدوائر ومعادلاتها. يمكن استخدامه لحساب مجموعة متنوعة من القياسات والمعادلات المتعلقة بالدوائر ويوفر تفاصيل هامة لفهم هذه الهندسة المهمة.
تحديد شعاع الدائرة
كيفية تحديد شعاع الدائرة وقيمته الرقمية
شعاع الدائرة هو المسافة بين مركز الدائرة ونقطة على حافتها الخارجية. يعد تحديد شعاع الدائرة أمرًا مهمًا في العديد من المجالات مثل الهندسة والرياضيات والعمارة والفيزياء والثقافة العامة. يتيح لك معرفة شعاع الدائرة فهم الشكل والأبعاد والخصائص المهمة للدائرة.
لتحديد شعاع الدائرة، يجب عليك قياس المسافة بين مركز الدائرة وأي نقطة على حافتها الخارجية. قطر الدائرة يعتبر مزدوجًا لشعاعها، ويمكن أيضًا استخدام قاعدة من أطراف الدائرة لتحديد الشعاع. قيمة شعاع الدائرة تكون بالنصف من قيمة القطر.
تعتبر الحسابات الرياضية والمعادلات الهندسية الأدوات المشتركة لتحديد قيمة شعاع الدائرة. باستخدام المعادلات الصحيحة والأدوات المناسبة، يمكنك بسهولة حساب قيمة شعاع الدائرة الرقمية.
في الختام، تحديد شعاع الدائرة يلعب دورًا هامًا في فهم وقياس الدوائر والأشكال المدورة. يتطلب ذلك استخدام المعادلات الرياضية والأدوات الملائمة لقياس وتحديد قيمة شعاع الدائرة بشكل صحيح.
العلاقة بين شعاع الدائرة ونصف قطرها
إذا كنت تسأل عن العلاقة بين شعاع الدائرة ونصف قطرها، فإنها تعتبر واحدة من المفاهيم الأساسية في الهندسة الهندسية. يتعلق الأمر بالعلاقة المباشرة بين الشعاع ونصف قطر الدائرة.
تفسير العلاقة بين شعاع الدائرة ونصف قطرها والتأثير على المساحة والمحيط
يعرف الشعاع في الدائرة بأنه الخط الذي يربط مركز الدائرة بأي نقطة على حافتها. بينما يتم تعريف النصف قطر على أنه المسافة من مركز الدائرة إلى أي نقطة على حافتها.
تتناسب الطولان مع بعضهما البعض. بمعنى آخر، يكون الشعاع ضعف طول النصف قطر. إذا كان لدينا شعاع بطول 2 وحدة، سيكون النصف قطر بطول واحدة.
تؤثر هذه العلاقة أيضًا على المساحة والمحيط للدائرة. إذا كان لدينا مثلاً نصف قطر بطول 4 وحدات، فإن المساحة ستكون 16π وحدة مربعة، والمحيط سيكون 8π وحدة.
فهم العلاقة بين شعاع الدائرة ونصف قطرها ضروري للتعامل مع الدوائر وحساب صفاتها بشكل دقيق وفعال. سواء كنت طالبًا للهندسة أو مهتمًا بالرياضيات، فإن معرفتك بهذه العلاقة ستكون قاعدة مهمة لتطبيقات أوسع في المستقبل.
المثال التطبيقي
تطبيق عملي يوضح استخدام شعاع الدائرة في حسابات الدوائر
في الرياضيات والفيزياء، تلعب المعادلات الدائرية دورًا هامًا في حسابات الدوائر والمنحنيات المنحنية. تُستخدم المعادلات الدائرية لتحديد مواقع النقاط على حلقة الدائرة ومعرفة الأبعاد الهندسية للدائرة مثل نصف القطر والقطر والمحيط والمساحة.
هنا يأتي دور شعاع الدائرة الذي يعتبر إحدى الأدوات الهامة في حسابات الدوائر. شعاع الدائرة هو الخط الذي يصل مركز الدائرة بأي نقطة على حلقتها. ببساطة، يُعرف شعاع الدائرة باسم نصف القطر وهو يساوي نصف القطر الذي يربط بين المركز وأي نقطة على حلقة الدائرة.
تطبيقًا عمليًا يوضح استخدام شعاع الدائرة في حسابات الدوائر هو حساب محيط الدائرة. لحساب المحيط، يمكن استخدام الصيغة العامة:
محيط الدائرة = 2 × نصف القطر × ط
حيث تُمثل “ط” قيمة ثابتة تُمثل نسبة محيط الدائرة إلى قطرها، وتقرب إلى قيمة تقريبية تساوي 3.14.
باستخدام شعاع الدائرة لتمثيل نصف القطر، يمكن حساب محيط الدائرة بسهولة باستخدام هذه الصيغة.
الخلاصة
يعد شعاع الدائرة مفهومًا هامًا في الهندسة الهندسة الرياضية. فهم هذا المفهوم ومعرفة كيفية استخدامه يمكن أن يكون ذو فائدة كبيرة للطلاب والمهندسين على حد سواء.
أهمية وفائدة فهم مفهوم واستخدامات شعاع الدائرة
فهم الشعاع: يعرف شعاع الدائرة بأنه الخط البادئ للقوس. فهم مفهوم الشعاع يمكن أن يفتح الباب أمام استكشاف المزيد من مفاهيم الهندسة الهندسة الرياضية.
استخدامات شعاع الدائرة: يتم استخدام شعاع الدائرة في العديد من الأمور، مثل قياس الزوايا واحتساب طول القوس. كما يمكن استخدامه لمعرفة المسافة بين نقطتين على الدائرة.
فهم هذا المفهوم واستخداماته يمكن أن يسهم في التفكير التحليلي وحل المشاكل الهندسية. يمكن استخدام المعرفة المكتسبة لتطبيقها في مجالات مختلفة مثل الهندسة المدنية والهندسة المعمارية.
باختصار، فهم مفهوم واستخدامات شعاع الدائرة يمكن أن يكون ذا فائدة كبيرة للكثير من الناس، سواء في الدراسة أو في مجالاتهم المهنية.