الفرق بين الأعداد النسبية وغير النسبية
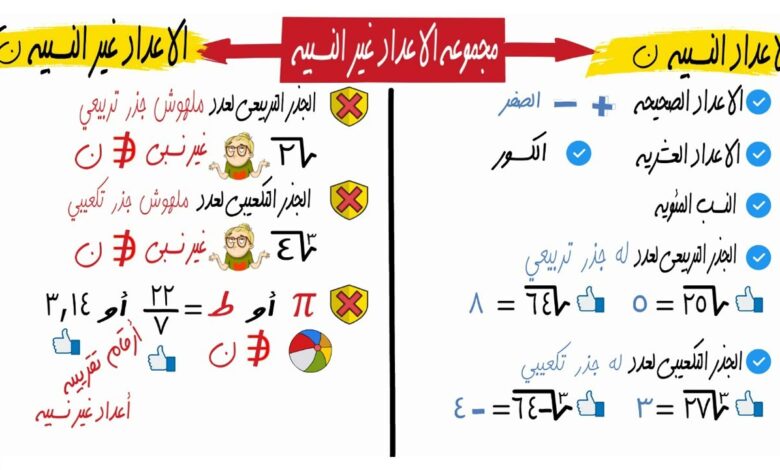
الأعداد النسبية وغير النسبية في الرياضيات هي الأعداد التي يمكن كتابتها على صورة كسر A/B، حيث A و B هما عددان صحيحان، و B لا يساوي صفر. وتشمل الأعداد النسبية الأعداد الصحيحة، والكسور الاعتيادية، والكسور العشرية المنتهية، والكسور العشرية الدورية. وفي السطور التالية نوضح كافة التفاصيل على موقع بسيط دوت كوم.
أما الأعداد غير النسبية فهي الأعداد التي لا يمكن كتابتها على صورة كسر A/B، حيث A و B هما عددان صحيحان، و B لا يساوي صفر. وتشمل الأعداد غير النسبية الجذور التربيعية للأعداد غير الكاملة، مثل جذر 2، وجذر 3، وجذر 5، وبعض الكسور العشرية غير الدورية مثل العدد π.
الفرق بين الأعداد النسبية وغير النسبية
- الأعداد النسبية هي مجموعة فرعية من الأعداد الحقيقية، بينما الأعداد غير النسبية ليست جزءًا من مجموعة الأعداد الحقيقية.
- يمكن تمثيل الأعداد النسبية ككسور، بينما لا يمكن تمثيل الأعداد غير النسبية ككسور.
- الأعداد النسبية لها خصائص مشابهة للأعداد الصحيحة، بينما تختلف الأعداد غير النسبية عن الأعداد الصحيحة في بعض الخصائص.
أمثلة على الأعداد النسبية
- الأعداد الصحيحة كلها أعداد نسبية.
- الكسور الاعتيادية كلها أعداد نسبية.
- ثم الكسور العشرية المنتهية كلها أعداد نسبية.
- ثم الكسور العشرية الدورية كلها أعداد نسبية.
أمثلة على الأعداد غير النسبية
- الجذور التربيعية للأعداد غير الكاملة مثل جذر 2، وجذر 3، وجذر 5.
- بعض الكسور العشرية غير الدورية مثل العدد π.
الخصائص الرياضية للأعداد النسبية
- يمكن الجمع، والطرح، والضرب، والقسمة على الأعداد النسبية.
- ثم تظل الأعداد النسبية نسبية عند الجمع، والطرح، والضرب.
- ثم تصبح الأعداد النسبية وغير النسبية عند القسمة على صفر.
التطبيقات العملية للأعداد النسبية
تستخدم الأعداد النسبية في العديد من التطبيقات العملية، مثل:
- الحساب والقياس.
- الهندسة والجبر.
- ثم الفيزياء والكيمياء.
- ثم الاقتصاد والمالية.
كيف اعرف ان العدد غير نسبي؟
العدد غير النسبي هو عدد لا يمكن كتابته على صورة كسر ﺃ على ﺏ، حيث ﺃ وﺏ عددان صحيحان وﺏ لا يساوي صفرًا. هناك عدة طرق لمعرفة إذا كان العدد غير نسبي:
- طريقة القسمة: يمكن قسمة العدد على جميع الأعداد الصحيحة الممكنة، إذا لم يتم الحصول على كسر صحيح، فإن العدد غير نسبي.
- طريقة التمثيل العشري: يمكن كتابة العدد في صورة كسر عشري، إذا كان التمثيل العشري غير منته أو متكرر، فإن العدد غير نسبي.
- ثم طريقة الجذر التربيعي: يمكن حساب الجذر التربيعي للعدد، إذا لم يكن الجذر التربيعي عددًا صحيحًا، فإن العدد غير نسبي.
أمثلة على الأعداد غير النسبية
فيما يلي بعض الأمثلة على الأعداد غير النسبية:
- جذور الأعداد غير المربعة: مثل جذر 2، جذر 3، جذر 5، إلخ.
- عدد باي (π): وهو ثابت رياضي يُستخدم لحساب محيط الدائرة.
- عدد أويلر (e): وهو ثابت رياضي يُستخدم في العديد من المجالات الرياضية.
- النسبة الذهبية (φ): وهي نسبة رياضية تُستخدم في العديد من المجالات الفنية والعلمية.
أمثلة على الأعداد النسبية
فيما يلي بعض الأمثلة على الأعداد النسبية:
- 1/2
- 3/4
- 5/6
- 7/8
- 9/10
من المهم ملاحظة أنه لا توجد طريقة حاسمة لتحديد ما إذا كان العدد غير نسبي، ولكن الطرق المذكورة أعلاه توفر طريقة جيدة للتحقق من ذلك.
أي الأعداد غير نسبي؟
العدد غير النسبي هو العدد الذي لا يمكن كتابته على صورة كسر ﺃ على ﺏ، حيث ﺃ وﺏ عددان صحيحان وﺏ لا يساوي صفرًا. وبتعبير آخر، العدد غير النسبي لا يمكن أن يُمثل على شكل كسر بسيط. ومن الأمثلة على الأعداد غير النسبية:
- الجذور التربيعية للأعداد الموجبة التي ليست مربعات كاملة. مثل الجذر التربيعي لـ 2، والجذر التربيعي لـ 3، والجذر التربيعي لـ 5.
- النسبة الذهبية φ، وهي النسبة بين طول ضلع مربع إلى طول ضلع مثلث متساوي الساقين.
- العدد π، وهو محيط الدائرة مقسومًا على قطرها.
- ثابت أويلر e، وهو ثابت رياضي يصف معدل النمو الأسي.
ويمكن التحقق من أن هذه الأعداد غير نسبية عن طريق إثبات أن تمثيلها العشري غير منته ولا متكرر. أما الفرق بين الأعداد النسبية وغير النسبية فهو أن العدد النسبي يمكن كتابته على صورة كسر ﺃ على ﺏ، بينما العدد غير النسبي لا يمكن كتابته على هذه الصورة. وبشكل عام، يمكن القول أن الأعداد غير النسبية هي الغالبية العظمى من الأعداد الحقيقية.
ما هي انواع الاعداد النسبية؟
يمكن تقسيم الأعداد النسبية إلى ثلاثة أنواع رئيسية:
- الأرقام الصحيحة: وهي الأعداد التي لا تحتوي على كسور، مثل 1، 2، 3، -1، -2، -3.
- الكسور البسيطة: وهي الأعداد التي يمكن كتابتها على شكل كسر، حيث يكون البسط عددًا صحيحًا، والمقام عددًا صحيحًا غير مساوي للصفر، مثل 2/3، 5/6، -2/3، -5/6.
- الكسور العشرية النهائية: وهي الأعداد العشرية التي تنتهي برقم معين، مثل 0.35، 0.7116، 0.9768.
الاعداد النسبية
بالإضافة إلى هذه الأنواع الثلاثة، يمكن تقسيم الأعداد النسبية إلى نوعين فرعيين:
- الأرقام النسبية الموجبة: وهي الأعداد التي لها نفس الإشارة في البسط والمقام، مثل 2/3، 5/6، 0.35، 0.7116، 0.9768.
- الأرقام النسبية السالبة: وهي الأعداد التي لها إشارات مختلفة في البسط والمقام، مثل -2/3، -5/6، -0.35، -0.7116، -0.9768.
خصائص الأعداد النسبية
- يمكن إضافة الأعداد النسبية وطرحها وضربها وقسمتها.
- ثم يمكن ترتيب الأعداد النسبية من الأصغر إلى الأكبر.
- ثم يمكن مقارنتها ببعضها البعض.
من اين تبدأ الاعداد الحقيقية؟
تبدأ الأعداد الحقيقية من الصفر، حيث يمثل الصفر نقطة التقاطع بين خط الأعداد الموجبة وخط الأعداد السالبة. وعلى خط الأعداد، تقع الأعداد الموجبة على يمين الصفر، وتقع الأعداد السالبة على يسار الصفر.
وبشكل أكثر تحديدًا، يمكن القول أن الأعداد الحقيقية تبدأ من الصفر، وتستمر إلى ما لا نهاية في كلا الاتجاهين، أي إلى الأعداد الموجبة وإلى الأعداد السالبة. وهذا يعني أن هناك عددًا لا نهائيًا من الأعداد الحقيقية، منها:
- الأعداد الصحيحة، مثل 1، 2، 3، 4، …
- ثم الأعداد الكسرية، مثل 1/2، 3/4، 1/3، …
- ثم الأعداد غير النسبية، مثل π، √2، e، …
وعلى الرغم من أن الأعداد الحقيقية تبدأ من الصفر، إلا أنه يمكننا أيضًا القول أنها تبدأ من أي عدد حقيقي آخر. فعندما نقول أن العدد 1 أكبر من العدد -1، فإننا نعني أن 1 يقع إلى يمين -1 على خط الأعداد.
وبنفس الطريقة، عندما نقول أن العدد π أكبر من العدد 3، فإننا نعني أن π يقع إلى يمين 3 على خط الأعداد. ولذلك، يمكننا القول أن الأعداد الحقيقية تبدأ من أي عدد حقيقي، وتستمر إلى ما لا نهاية في كلا الاتجاهين.
ما هو الفرق بين العدد الصحيح والعدد الحقيقي؟
ضمن الحديث عن الأعداد النسبية وغير النسبية الفرق بين العدد الصحيح والعدد الحقيقي هو أن العدد الصحيح هو عدد لا يحتوي على أجزاء كسريّة، بينما العدد الحقيقي هو أي عدد يمكن تمثيله على خط الأعداد، بما في ذلك الأعداد الصحيحة والكسور.
بشكل أكثر تحديدًا، يمكن تعريف العدد الصحيح على أنه عدد يمكن كتابته بدون استخدام الكسور أو الفواصل العشرية. ويشمل الأعداد الطبيعية (1، 2، 3، …) والصفر والأعداد السالبة المقابلة للأعداد الطبيعية (-1، -2، -3، …).
أما العدد الحقيقي فهو أي عدد يمكن تمثيله على خط الأعداد، بما في ذلك الأعداد الصحيحة والكسور. ويشمل الأعداد الصحيحة والكسور والأرقام غير النسبية، مثل √2 و π.
أمثلة على الأعداد الصحيحة
فيما يلي بعض الأمثلة على الأعداد الصحيحة:
- عدد المقاعد في الصف الواحد في الفصل الدراسي.
- عدد الطلاب في المدرسة.
- ثم عدد الأيام في الشهر.
- ثم عدد الساعات في اليوم.
أمثلة على الأعداد الحقيقية
فيما يلي بعض الأمثلة على الأعداد الحقيقية:
- طول قطعة من الخشب
- وزن شخص
- ثم درجة الحرارة
- ثم الوقت.
جدير بالذكر يمكن القول أن العدد الصحيح هو مجموعة فرعية من مجموعة الأعداد الحقيقية. وتتميز الأعداد الصحيحة بأنها لا تحتوي على أجزاء كسريّة، بينما تشمل الأعداد الحقيقية الأعداد الصحيحة والكسور والأرقام غير النسبية.
هل الصفر ينتمي لمجموعة الاعداد الحقيقية؟
نعم، الصفر ينتمي لمجموعة الأعداد الحقيقية. مجموعة الأعداد الحقيقية هي مجموعة من جميع الأعداد التي يمكن العثور عليها على خط الأعداد، وهي تشمل الأعداد النسبية وغير النسبية، والموجبة والسالبة، وحتى الصفر. ثم يمكن تعريف الصفر بأنه عدد حقيقي ليس موجبًا وليس سالبًا. إنه نقطة التقاطع بين المحورين السالب والموجب على خط الأعداد.
يمكن أيضًا تعريف الصفر بأنه عدد حقيقي يكون مجموع أي عدد حقيقي معه هو نفس العدد الحقيقي. على سبيل المثال، 0 + 5 = 5. وبالتالي، فإن الصفر ينتمي لمجموعة الأعداد الحقيقية لأنه يلبي تعريفات مجموعة الأعداد الحقيقية.
هل الاعداد الحقيقية سالبة؟
نعم، يمكن أن تكون الأعداد الحقيقية سالبة. حيث أن الأعداد الحقيقية هي مجموعة من الأعداد التي يمكن تمثيلها على خط الأعداد، ويمكن أن تكون هذه الأعداد صحيحة أو كسورية، موجبة أو سالبة، فالمهم أن يكون مربّعها حقيقيًا موجبًا.
الأعداد السالبة هي أعداد حقيقية أصغر من الصفر، مثل -2، -5، -100، إلخ. يتم تمثيل الأعداد السالبة على خط الأعداد إلى يسار الصفر. إليك بعض الأمثلة على الأعداد الحقيقية السالبة:
- درجة الحرارة في الخارج هي -10 درجة مئوية.
- مديونية شخص ما هي 1000 دولار.
- ارتفاع شخص ما هو 165 سم.
لذلك، يمكننا القول أن الأعداد الحقيقية يمكن أن تكون سالبة، ويمكن استخدامها لتمثيل مجموعة متنوعة من القيم، مثل درجات الحرارة، والمبالغ المالية، والأبعاد.
ما هي الأعداد الطبيعية والصحيحة والنسبية؟
الأعداد الطبيعية هي الأعداد التي تبدأ من 1 وتستمر إلى ما لا نهاية، وهي لا تشمل الأعداد السالبة أو الصفر. ويرمز لمجموعة الأعداد الطبيعية بالحرف اللاتيني N. الأعداد الصحيحة هي الأعداد التي تشمل الأعداد الطبيعية والسالبة والصفر. ويرمز لمجموعة الأعداد الصحيحة بالرمز Z.
الأعداد النسبية هي الأعداد التي يمكن كتابتها على شكل كسر، حيث يكون بسط الكسر عددًا صحيحًا، ومقامه عددًا صحيحًا غير صفري. ويرمز لمجموعة الأعداد النسبية بالرمز Q. العلاقات بين الأعداد الطبيعية والصحيحة والنسبية:
- جميع الأعداد الطبيعية هي أعداد صحيحة.
- ثم جميع الأعداد الصحيحة غير السالبة هي أعداد طبيعية.
- ثم جميع الأعداد النسبية هي أعداد صحيحة أو أعداد طبيعية.
أمثلة على الأعداد الطبيعية والصحيحة والنسبية
ضمن الحديث عن الأعداد النسبية وغير النسبية سوف نتحدث في السطور التالية عن أمثلة على الأعداد الطبيعية والصحيحة والنسبية:
- الأعداد الطبيعية: 1، 2، 3، 4، 5، …
- ثم الأعداد الصحيحة: -5، -4، -3، -2، -1، 0، 1، 2، 3، 4، 5، …
- ثم الأعداد النسبية: 1/2، 1/3، 2/3، -1/2، -1/3، -2/3، 0.5، 0.3333…، -0.5، -0.3333…
استخدامات الاعداد الصحيحة الطبيعية
- تستخدم الأعداد الطبيعية في العد والقياس.
- ثم تستخدم الأعداد الصحيحة في العمليات الحسابية.
- ثم تستخدم الأعداد النسبية في التعبير عن الأجزاء من الكل.
- الأعداد الطبيعية هي الأعداد التي تبدأ من 1 وتستمر إلى ما لا نهاية.
- ثم الأعداد الصحيحة هي الأعداد التي تشمل الأعداد الطبيعية والسالبة والصفر.
- ثم الأعداد النسبية هي الأعداد التي يمكن كتابتها على شكل كسر.
ما هي الأعداد الصحيحة والحقيقية والطبيعية؟
الأعداد الصحيحة هي مجموعة من الأعداد التي يمكن كتابتها بدون استخدام الكسور أو الفواصل العشرية. وتتكون مجموعة الأعداد الصحيحة من الأعداد الطبيعية (1، 2، 3.) والصفر والأعداد السالبة المقابلة للأعداد الطبيعية (-1، -2، -3..)
الأعداد الطبيعية هي مجموعة من الأعداد التي تبدأ بالرقم 1 وتستمر إلى ما لا نهاية. وتستخدم الأعداد الطبيعية لوصف الكميات المتناهية، مثل عدد الأشياء أو عدد المرات.
الأعداد الحقيقية هي مجموعة من الأعداد التي يمكن كتابتها باستخدام الكسور أو الفواصل العشرية. وتتكون مجموعة الأعداد الحقيقية من الأعداد الصحيحة والكسرية.
أنواع الاعداد الصحيحة الطبيعية
فيما يلي شرح أكثر تفصيلاً لكل نوع من أنواع الأعداد:
الأعداد الصحيحة
- يمكن كتابتها بدون استخدام الكسور أو الفواصل العشرية.
- تتكون من الأعداد الطبيعية والصفر والأعداد السالبة.
- ثم الأعداد الطبيعية هي مجموعة فرعية من الأعداد الصحيحة.
- ثم الأعداد السالبة هي الأعداد الصحيحة التي تقل عن الصفر.
ما هي الأعداد الطبيعية؟
- تبدأ بالرقم 1 وتستمر إلى ما لا نهاية.
- ثم تستخدم لوصف الكميات المتناهية، مثل عدد الأشياء أو عدد المرات.
- ثم الأعداد الطبيعية هي مجموعة فرعية من الأعداد الصحيحة.
الأعداد الحقيقية
- يمكن كتابتها باستخدام الكسور أو الفواصل العشرية.
- تتكون من الأعداد الصحيحة والكسرية.
- ثم الأعداد الصحيحة هي مجموعة فرعية من الأعداد الحقيقية.
- ثم الأعداد الكسرية هي الأعداد التي يمكن كتابتها ككسر، مثل 1/2 أو 3/4.
أمثلة الاعداد الصحيحة الطبيعية
- أمثلة على الأعداد الصحيحة: 1، 2، 3، -1، -2، -3
- ثم أمثلة على الأعداد الطبيعية: 1، 2، 3، 4، 5
- ثم أمثلة على الأعداد الحقيقية: 1، 2، 3، -1، -2، -3، 1/2، 3/4، π، √2
استخدامات الأعداد
ضمن الحديث عن الأعداد النسبية وغير النسبية تستخدم الأعداد في مجموعة متنوعة من المجالات، بما في ذلك الرياضيات والعلوم والهندسة والتجارة كما يلي:
- في الرياضيات، تستخدم الأعداد لوصف الكميات والعلاقات.
- في العلوم، تستخدم الأعداد لوصف البيانات والنتائج.
- ثم في الهندسة، تستخدم الأعداد لحساب القياسات والأبعاد.
- ثم في التجارة، تستخدم الأعداد لحساب الأسعار والكميات.
ما هي الاعداد الصحيحة والغير صحيحة؟
في الرياضيات، العدد الصحيح هو العدد الذي يمكن كتابته بدون استخدام الكسور أو الفواصل العشرية. تتكون مجموعة الأعداد الصحيحة من الأعداد الطبيعية (1، 2، 3.) والصفر والأعداد السالبة المقابلة للأعداد الطبيعية (-1، -2، -3..)
الأعداد الصحيحة
- الأعداد الصحيحة الموجبة: هي الأعداد التي أكبر من الصفر، مثل 1، 2، 3، 4، …
- ثم الأعداد الصحيحة السالبة: هي الأعداد التي أصغر من الصفر، مثل -1، -2، -3، -4، …
- الصفر: هو العدد الصحيح الوحيد الذي ليس موجبًا ولا سالبًا.
الأعداد غير الصحيحة
- الأعداد الكسرية: هي الأعداد التي يمكن كتابتها على شكل كسر، مثل 1/2، 3/4، 5/6، …
- ثم الأعداد العشرية: هي الأعداد التي يمكن كتابتها على شكل عدد عشري، مثل 1.2، 3.45، 5.678، …
- الأعداد التخيلية: هي الأعداد التي تحتوي على جذر تربيعي سالب، مثل √-1، √-2، √-3، …
الفرق بين الاعداد الصحيحة الطبيعية والغير صحيحة
ضمن الحديث عن الأعداد النسبية وغير النسبية يمكن تمييز الأعداد الصحيحة عن الأعداد غير الصحيحة من خلال الخصائص التالية:
- الكتابة: يمكن كتابة الأعداد الصحيحة بدون استخدام الكسور أو الفواصل العشرية، بينما لا يمكن كتابة الأعداد غير الصحيحة بهذه الطريقة.
- الإشارة: الأعداد الصحيحة لها إشارة، إما موجبة أو سالبة، بينما لا تحتوي الأعداد غير الصحيحة على إشارة.
- العمليات الحسابية: مجموعة الأعداد الصحيحة منغلقة تحت عمليتي الجمع والضرب، بينما مجموعة الأعداد غير الصحيحة منغلقة تحت جميع العمليات الحسابية.
ما معنى كلمة عدد عشري؟
كلمة “عدد عشري” تعني عددًا يمكن كتابته بالضبط بعدد منتهي الأرقام بعد الفاصلة، بواسطة نظام العد الهندي العربي. الأعداد العشرية عبارة عن قسمة عدد صحيح بواسطة رفع 10 وتمثل على شكل عدد كسري. يمكن كتابة الأعداد العشرية بعدة طرق، منها:
- الطريقة التقليدية: وهي كتابة العدد بالأرقام العربية، مع وضع الفاصلة العشرية بين الجزء الصحيح والجزء العشري.
- الطريقة الكسورية: وهي كتابة العدد على شكل عدد صحيح مقسوم على 10 مرفوع إلى قوة معينة، بحيث تكون هذه القوة مساوية لعدد الأرقام الموجودة بعد الفاصلة العشرية.
- ثم الطريقة العلمية: وهي كتابة العدد على شكل عدد صحيح مضروب في 10 مرفوع إلى قوة معينة، بحيث تكون هذه القوة موجبة إذا كان الجزء العشري موجبًا، وسلبية إذا كان الجزء العشري سالبًا.
طرق حساب الأعداد العشرية
بعض الأمثلة على الأعداد العشرية:
- الطريقة التقليدية: 2.5، 13.76، -0.09
- ثم الطريقة الكسورية: 25/10، 1376/1000، -9/100
- الطريقة العلمية: 2.5 × 10^1، 1.376 × 10^-2، -9 × 10^-2.
الأعداد العشرية قراءة وكتابة
الأعداد العشرية هي الأعداد التي تتكون من عدد صحيح وجزء عشري. يُقسم العدد العشري باستخدام الفاصلة العشرية إلى قسمين:
- الجزء الصحيح: وهو الجزء الموجود على يسار الفاصلة العشرية.
- الجزء العشري: وهو الجزء الموجود على يمين الفاصلة العشرية.
قراءة الأعداد العشرية
- يقرأ العدد العشري بقراءة الجزء الصحيح ثم الجزء العشري.
- الجزء الصحيح يُقرأ كما هو.
- الجزء العشري يُقرأ بإضافة كلمة “عشر” أو “عشرات” أو “مئات” أو “آلاف” أو ما إلى ذلك، حسب موضع الرقم في الجزء العشري.
أمثلة على الاعداد العشرية للصف الرابع الخامس
- العدد 1.2 يُقرأ “واحد وعشرون”.
- العدد 3.5 يُقرأ “ثلاثة وخمسون”.
- ثم العدد 4.72 يُقرأ “أربعة وسبعون وعشرون”.
- ثم العدد 5.000 يُقرأ “خمسة آلاف”.
كتابة الأعداد العشرية الصف الرابع
يكتب العدد العشري بكتابة الجزء الصحيح ثم الجزء العشري، مع وضع الفاصلة العشرية بينهما.
- الجزء الصحيح يُكتب بدون فاصلة.
- الجزء العشري يُكتب بعد الفاصلة العشرية.
الأعداد النسبية والأعداد غير النسبية
الأعداد النسبية هي الأعداد التي يمكن كتابتها على شكل كسر، حيث يكون البسط عددًا صحيحًا، والمقام عددًا صحيحًا غير مساوي للصفر. أما الأعداد غير النسبية فهي الأعداد التي لا يمكن كتابتها على شكل كسر، مثل جذر 2، جذر 3، π.
هل الصفر عدد نسبي او غير نسبي؟
الصفر هو عدد نسبي. العدد النسبي هو عدد يمكن كتابته على صورة كسر ﺃ على ﺏ، حيث ﺃ وﺏ عددان صحيحان وﺏ لا يساوي صفرًا. في حالة الصفر، يمكن كتابته على الصورة 0/1، حيث ﺃ = 0 وﺏ = 1. وبالتالي، فإن الصفر هو عدد نسبي.
يمكن أيضًا إثبات أن الصفر هو عدد نسبي باستخدام تعريف الأعداد النسبية على أنها الأعداد التي لها تمثيل عشري منته أو متكرر. الصفر له تمثيل عشري منته، وهو 0.0000…، حيث تنتهي الأرقام صفر بعدد لا نهائي من المنازل العشرية. وبالتالي، فإن الصفر هو عدد نسبي.
قد يهمك





