ماهو المدى
ما هو المدى؟
مفهوم المدى واستخداماته
في عالم الإحصاء، يُعرف المدى بأنه مقياس يستخدم لتحديد انتشار القيم في مجموعة بيانات. وببساطة، يتم حساب المدى عن طريق تحديد الفرق بين أكبر قيمة وأصغر قيمة في البيانات. يعتبر المدى مقياساً سريعاً وبسيطاً لقياس التباين في البيانات.
تُستخدم العديد من الاستخدامات للمدى في عالم الإحصاء والبحوث، بما في ذلك:
- تحليل البيانات: يساعد المدى في فهم كيفية توزيع البيانات في مجموعة محددة، ومعرفة ما إذا كانت البيانات متنوعة أم توجد تجمعات أو تناثر.
- المقارنة بين مجموعات: يمكن استخدام المدى لمقارنة قيمة محددة في مجموعة من البيانات مع قيمة مماثلة في مجموعة أخرى.
- تحليل الأنماط: يمكن استخدام المدى لكشف أنماط التغير في البيانات عبر الوقت أو المكان.
حساب المدى لعدد من القيم
لحساب المدى، يجب أن تكون لديك مجموعة من القيم العددية. قم بترتيب هذه القيم بترتيب تصاعدي، ثم اطرح القيمة الأصغر من القيمة الأكبر. الفرق بين القيمتين هو المدى.
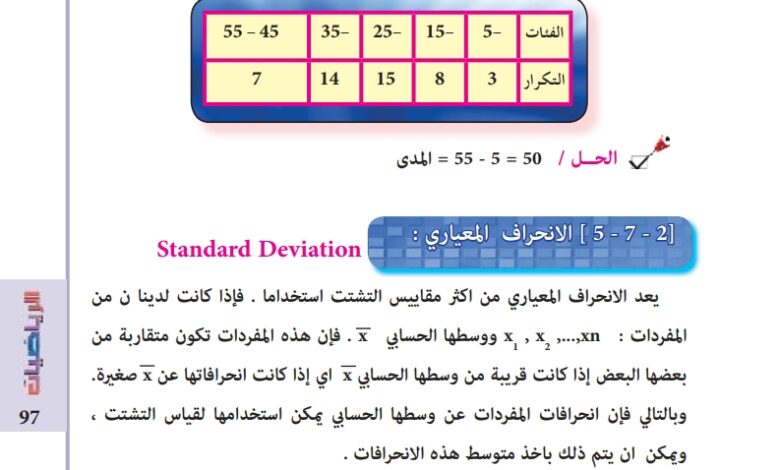
على سبيل المثال، لو كانت لديك مجموعة من الأعمار التالية: 25، 30، 35، 40، 45، 50، 55، فإن القيمة الأكبر هي 55 والقيمة الأصغر هي 25. لذا، المدى هو 55 – 25 = 30.
يعتبر المدى أداة مفيدة في تحليل البيانات وفهم التباين في القيم. ومع فهمك لمفهوم المدى وكيفية حسابه، يمكنك استخدامه في عملك أو في دراساتك لاستكشاف بياناتك الرقمية واكتشاف الأنماط والتغيرات.
كيفية حساب المدى
باختصار، المدى هو فقط فرق بين القيمتين الأقصى والأدنى في مجموعة من الأرقام. لحساب المدى، يجب على الشخص أولاً ترتيب الأرقام بترتيب تصاعدي، ثم يقوم بطرح القيمة الأدنى من القيمة الأقصى.
مثال توضيحي لحساب المدى
على سبيل المثال، لدينا مجموعة من الأرقام التالية: 5، 8، 2، 10، 6، 7. لحساب المدى، يجب أن نرتب هذه الأرقام بترتيب تصاعدي، لذا ستكون كالتالي: 2، 5، 6، 7، 8، 10. بعد ذلك، نقوم بطرح القيمة الأدنى (2) من القيمة الأقصى (10). يكون المدى في هذا المثال هو 8.
أهمية مقياس المدى في تحليل البيانات
مقياس المدى يلعب دورًا هامًا في تحليل البيانات. إليك بعض الأسباب التي تبرز أهمية حساب المدى:
- يوضح انتشار البيانات: المدى يساعد في فهم مدى تفاوت البيانات ومدى تشتتها بين القيم.
- يساعد في تحديد القيم الشاذة: عندما يكون المدى كبيرًا، فإن القيم الشاذة يمكن أن تتضمن قيمًا تقع بعيدًا عن المعتاد.
- يعمل كمقياس بسيط: يمكن استخدام المدى كمقياس بسيط لتقييم الفروق بين الأرقام في مجموعة البيانات.
باختصار، حساب المدى يساعدنا على فهم توزيع البيانات وإبراز القيم الشاذة، مما يجعله أداة مهمة في تحليل البيانات.
المدى ومقاييس النزعة المركزية الأخرى
المدى هو مقياس في التحليل الإحصائي يستخدم لقياس انتشار البيانات. يُعرف المدى بأنه الفرق بين أكبر وأصغر قيمة في مجموعة من البيانات. على سبيل المثال، إذا كانت هناك مجموعة من الأعمار تتراوح بين 20 و 30 عامًا، فإن المدى سيكون 10 سنوات.
الاختلافات بين المدى والوسيط والمتوسط والمنوال
- المدى: يعطي معلومات حول توزع البيانات وانتشارها، ولكنه لا يوفر معلومات حول القيمة المركزية للبيانات.
- الوسيط: يعكس القيمة المركزية للبيانات ويمثل القيمة التي يقع بها النصف الأعلى والنصف الأدنى.
- المتوسط: يمثل القيمة المتوسطية للبيانات بجمع جميع القيم ثم قسمتها على عددها.
- المنوال: يعطي معلومات عن توزع البيانات حول الوسيط ويعكس قيمة اعتدالها.
إيجابيات وسلبيات استخدام المدى في التحليل الإحصائي
- إيجابيات المدى:
- سهولة حسابه وفهمه.
- يعطي فكرة عن توسع البيانات.
- سلبيات المدى:
- يتأثر بقيم الطرفين في المجموعة، ولا يوفر معلومات تفصيلية عن توزع البيانات.
- يتأثر بالقيم المتطرفة في المجموعة، ولا يمثل قيمة مركزية للبيانات.
بشكل عام، يُعتبر المدى أداة مهمة في تحليل البيانات الإحصائية، ولكنه يجب استخدامه بجانب مقاييس أخرى للحصول على صورة أكثر اكتمالًا عن البيانات.
أمثلة عملية لحساب المدى
توضيح الطريقة المناسبة لحساب المدى
عندما يتعلق الأمر بحساب المدى، فإنه من المهم استخدام الطريقة المناسبة للحصول على نتائج دقيقة. هناك طريقتان شائعتان لحساب المدى:
- الطريقة البسيطة: تعتمد هذه الطريقة على اختلاف القيمة العلوية والقيمة السفلية في مجموعة البيانات. على سبيل المثال، إذا كانت القيم العلوية هي 10 والقيمة السفلية هي 2، فإن المدى سيكون 10 – 2 = 8.
- الطريقة المتقدمة: تستخدم هذه الطريقة الإحصاء لتحليل مجموعة البيانات بشكل أعمق. يتم حساب المدى في هذه الحالة عن طريق تحديد القيمة الأكثر تكرارًا والقيمة الأقل تكرارًا في المجموعة، ثم يتم حساب الفرق بينهما.
تحليل ثلاثة أمثلة مختلفة لحساب المدى
سنوضح الآن ثلاثة أمثلة لحساب المدى باستخدام الطريقة المتقدمة:
- مجموعة أصوات الطلاب في الفصل: إذا كانت قيم الصوت التي تسجلت هي 60، 65، 70، 70، 75، 80، 80، 85، 85، 90، فإن القيمة الأقل تكرارًا هي 60 والقيمة الأعلى تكرارًا هي 90. بالتالي، يكون المدى هو 90 – 60 = 30.
- درجات الطلاب في امتحان الرياضيات: إذا كانت درجات الطلاب هي 75، 80، 85، 90، 95، 100، فإن القيمة الأقل تكرارًا هي 75 والقيمة الأعلى تكرارًا هي 100. بالتالي، يكون المدى هو 100 – 75 = 25.
- إيرادات الشركة خلال الأشهر الستة الأخيرة: إذا كانت الإيرادات هي 10000، 15000، 20000، 25000، 30000، 35000، فإن القيمة الأقل تكرارًا هي 10000 والقيمة الأعلى تكرارًا هي 35000. بالتالي، يكون المدى هو 35000 – 10000 = 25000.
الاستنتاجات والتوصيات
بعد النظرة العامة على المدى واستخداماته، يمكن التوصل إلى عدد من الاستنتاجات والتوصيات الهامة. إليك بعضها:
استخدامات المدى في مجالات مختلفة
- المدى يعتبر من المفاهيم المهمة في مجال التخطيط الاستراتيجي وإدارة المشاريع؛ حيث يساعد في تحديد أهداف المشروع والخطوات اللازمة لتحقيقها.
- في مجال الأعمال، يمكن استخدام المدى لتحديد نطاق النشاط التجاري والمناطق المستهدفة؛ مما يساعد في تحسين استراتيجيات التسويق وتوجيه الجهود بشكل أفضل.
- في مجال التخطيط العمراني وتطوير المدن، يمكن استخدام المدى لتحديد المساحات العمرانية المستقبلية وتوجيه عمليات التطوير والتخطيط العمراني.
مجموعة من النصائح والتوصيات عند استخدام مفهوم المدى.
- قبل تحديد المدى، يجب تحليل البيئة وفهم المحيط المحيط بالمشروع أو الأعمال؛ لتحديد الفرص والتحديات المحتملة.
- ينصح بتحديد مدى واقعي ومناسب للمشروع أو الأعمال، بالاعتماد على معايير ومعلومات ثابتة ودقيقة.
- قم بإعداد خطة واضحة لتنفيذ المدى، مع تحديد الخطوات والمدة الزمنية والموردين والموارد اللازمة لتحقيقه.
- يُوصى بمراقبة ومتابعة المدى بشكل منتظم، وإجراء تعديلات وتحسينات عند الحاجة.
- قم بالتواصل والتعاون مع الفرق المعنية داخل المنظمة لضمان تنفيذ المدى بنجاح.
باستخدام هذه النصائح والتوصيات، يمكن تحقيق أقصى استفادة من تطبيق مفهوم المدى في المجالات المختلفة.